Matematica per gli insegnanti
La differenza tra due numeri dei quali il primo (minuendo) è maggiore o
uguale al secondo (sottraendo), è un terzo numero (differenza) che addizionato
al secondo dà come somma il primo.
L’operazione necessaria per calcolare la differenza tra due numeri si
chiama sottrazione.
Se eseguiamo una sottrazione tra due numeri appartenenti ad
N, vediamo che la differenza è un numero appartenente ad N solo se il minuendo
è maggiore o uguale al sottraendo. Se il minuendo è minore del sottraendo, la
differenza non è in N: possiamo dunque dire che la
sottrazione non è un’operazione interna all’insieme N oppure che l’insieme
N è aperto rispetto alla sottrazione.
Abbiamo visto
che nella sottrazione, se il minuendo è minore del sottraendo, non è possibile
eseguire l’operazione in N. E’ quindi necessario allargare l’ambito numerico
considerando non solo i numeri interi positivi, ma introducendo anche i numeri
interi negativi.
N+ +
N- formano l’insieme dei numeri interi
relativi, detto insieme Z.
Matematica per gli alunni
COMPETENZE
|
ABILITA’
|
UNITA’
DI APPRENDIMENTO
|
Ricerca dati per ricavare informazioni e costruisce rappresentazioni
(tabelle e grafici).
Si muove con sicurezza nel calcolo scritto e mentale con i numeri
naturali e sa valutare l’opportunità di ricorrere a una calcolatrice.
|
- Al termine della classe terza l'alunno dovrà:
comprendere il significato dei numeri 1 e 0
nella sottrazione; individuare alcune caratteristiche della sottrazione;
leggere e rappresentare relazioni e dati con diagrammi, schemi e tabelle.
|
PERCORSO DIDATTICO
Rivediamo i termini della sottrazione: a questo proposito potrebbe essere utile una mia presentazione in PowerPoint con i "numeri uccelli".
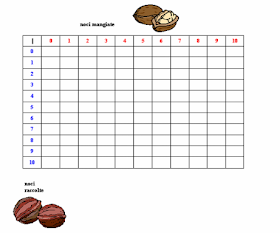
Proponiamo poi una tabella vuota da completare oppure facciamola rappresentare sul quaderno. Fai clic per stampare la tabella.
Lasciamo vuota per ora la prima casella in alto a sinistra e nella prima colonna scriviamo in blu il numero delle noci che Br1 ha raccolto. Prima non ne aveva, poi ne ha raccolto una, quindi 2, 3, ecc. Nella prima riga scriviamo in rosso il numero delle noci che invece voleva mangiare quel ghiottone di Bass8.
Ora, usando questa tabella, siamo in grado di sapere quante noci avevano i due amici in ogni momento. Ad esempio se Bruno ha raccolto 4 noci e Bassotto ne voleva mangiare una, quante noci sarebbero rimaste? Dove lo scriviamo? Quando Bruno aveva raccolto 5 noci, se Bassotto non ne aveva ancora mangiate, quante noci avevano? Ma allora che segno dovremo mettere nella cella in alto a sinistra che avevamo lasciata vuota? Certo, il segno - perché Bass8, mangiando le noci, ne fa diminuire la quantità. Riflettiamo: quando Bruno aveva raccolto 6 noci, Bassotto avrebbe potuto mangiarne 8? Perché? Secondo voi, ora la tabella è ancora quasi vuota, riusciremo a riempirla tutta? Perché? Proviamo, cominciando insieme per favorire la comprensione degli incroci tra righe e colonne e poi facendo proseguire gli alunni da soli.
Al termine scateniamo la caccia alle osservazioni, che trascriveremo in calce alla tabella stessa. Dovrebbe emergere:
• Non abbiamo riempito tutte le caselle, la sottrazione non è sempre possibile.
• La sottrazione con numeri naturali è possibile solo se il minuendo è maggiore o uguale al sottraendo
• Osservando la prima colonna ci accorgiamo che i numeri non sono cambiati, infatti se da un numero tolgo zero, il risultato non cambia. Lo zero è l’elemento neutro dell’addizione, quando è il sottraendo.
• Se da un numero togli 1, trovi il numero precedente
• Su una diagonale ci sono tutti “0” perché in una sottrazione se il minuendo è uguale al sottraendo, il resto è sempre “0
• La sottrazione non gode della proprietà commutativa. Possiamo allora mettere la freccia a doppia punta nella prima casella?
Propongo a questo punto un esercizio in cui gli alunni dovranno completare due piccole tabelle con la sottrazione, colorando le caselle in cui non sarà possibile eseguire le sottrazioni. Se vuoi stampare le tabelle (tre per foglio) fai clic qui.
Una verifica scritta da stampare
Un test sui contenuti dell'unità n° 3: la sottrazione
Una lezione per Lim sulle osservazioni a proposito della tabella della sottrazione
Un test sui contenuti dell'unità n° 3: la sottrazione
Una lezione per Lim sulle osservazioni a proposito della tabella della sottrazione