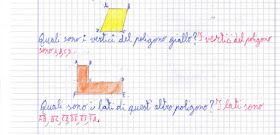Anche stavolta rendiamo partecipi gli alunni dei traguardi da raggiungere al completamento dell'unità di apprendimento ed elenchiamoli sul quaderno.
Al termine del settimo percorso "Il mare" dovrai aver imparato a:
• Conoscere i poligoni e le loro caratteristiche
• Risolvere problemi con la domanda nascosta
• Scomporre e trasformare le misure di massa
Matematica per gli insegnanti
Poligono è detta quella parte di piano delimitata da una linea spezzata chiusa.
I segmenti che formano la linea spezzata si dicono lati del poligono, gli estremi dei segmenti vertici, gli angoli formati da due segmenti consecutivi sono gli angoli interni del poligono.
Il segmento che collega due vertici non consecutivi si chiama diagonale del poligono.
La linea spezzata è il contorno del poligono e la misura del contorno è il perimetro.
Un poligono con tutti i lati congruenti si dice equilatero.
Un poligono con tutti gli angoli di uguale ampiezza si dice equiangolo.
Un poligono equilatero ed equiangolo si dice regolare.
In base al numero dei lati i poligoni prendono nomi diversi:
3 lati
|
triangolo
|
4 lati
|
quadrilatero
|
5 lati
|
pentagono
|
6 lati
|
esagono
|
7 lati
|
ettagono
|
8 lati
|
ottagono
|
9 lati
|
ennagono
|
10 lati
|
decagono
|
Se un poligono non contiene nessun prolungamento dei suoi lati è detto convesso; se contiene il prolungamento di uno o più lati si dice concavo.
Vediamo ora alcune proprietà dei poligoni
Se un poligono ha n lati (n sta per un qualunque numero), avrà anche n vertici, n angoli interni, n angoli esterni. Per ogni vertice ci saranno (n – 3) diagonali, quindi un triangolo non avrà diagonali (3 – 3 = 0), un quadrato ne avrà (4 – 3 = 1) per ogni vertice, un esagono avrà (6 – 3) diagonali per ogni vertice.
Immaginiamo ora di percorrere il contorno del seguente poligono partendo dal vertice A.
Tutti gli angoli che incontriamo percorrendo in senso antiorario il poligono una sola volta, formati da un lato e dal prolungamento del lato consecutivo si dicono angoli esterni del poligono.
La somma degli angoli esterni di un qualunque poligono, indipendentemente dal numero dei lati, corrisponde sempre ad un angolo giro, quindi misura 360°.
a + b + d + e + g = 360°
L’angolo esterno e quello interno con il vertice in comune sono adiacenti e quindi supplementari
d + l = 180 °
La somma degli angoli interni di un poligono di n lati corrisponde sempre a (n – 2) angoli piatti.
Quindi la somma degli angoli interni di un poligono di 5 lati sarà = (5 – 2) x 180° = 3 x 180° = 540°
Un’ultima annotazione: in un poligono ogni lato è sempre minore della somma dei restanti lati.
Matematica per gli alunni
COMPETENZE
|
ABILITA’
|
UNITA’
DI APPRENDIMENTO
|
L’alunno riconosce e rappresenta forme del
piano e dello spazio, relazioni e strutture che si trovano in natura o che
sono state create dall’uomo. Descrive,
denomina e classifica figure in base a caratteristiche geometriche, ne
determina misure, progetta e costruisce modelli concreti di vario tipo. Utilizza
strumenti per il disegno geometrico (riga, compasso, squadra) e i più comuni
strumenti di misura (metro, goniometro...).
|
- Al termine della classe terza l'alunno dovrà:
riconoscere, denominare e descrivere figure geometriche; disegnare figure geometriche e costruire
modelli materiali anche nello spazio; denominare e descrivere alcune
fondamentali figure geometriche del piano e dello spazio; conoscere ed
utilizzare la terminologia e le definizioni specifiche relative ai poligoni.
|
PERCORSO DIDATTICO
Tra tutte le cose che Br1 e Bass8 hanno visto sulla Terra, due sono le cose che più li hanno lasciati a bocca aperta: l’azzurro del cielo determinato dall’atmosfera terrestre ed il mare, sempre in movimento, con i colori cangianti da un momento all’altro.
E proprio al mare i due nostri amici
sono andati, per cercare di conoscerlo meglio. Eccoli sulla spiaggia, dove si
divertono a riconoscere le impronte sulla sabbia. Ecco alcune delle impronte
che hanno visto e che vi disegnerò alla lavagna.
Vediamo a
chi potrebbero appartenere queste impronte e notiamo: la prima impronta è
delimitata da linee curve, la seconda da una linea
spezzata chiusa e la terza da una linea mista . Scriviamo che solo le figure delimitate da linee spezzate
chiuse sono dette poligoni.
La prima e l'ultima figura non sono poligoni, la figura in mezzo è un poligono. Riconosciamo nella realtà
poligoni e proviamo a costruirne col geopiano.
Ogni
segmento della linea spezzata chiusa viene chiamato lato, mentre i punti
estremi di ogni lato sono chiamati vertici. Constatiamo che ogni poligono ha ugual numero di lati, vertici
ed angoli.
I vertici
dei poligoni sono indicati con lettere maiuscole ed i lati con le lettere dei
vertici che li individuano.
Proponiamo un piccolo esercizio
Consideriamo
ora questi due poligoni e proviamo a tracciare dei segmenti che uniscano due punti della regione interna
dello stesso colore.
Ci
accorgiamo che nel primo poligono nessun segmento attraversa il confine, mentre
nel secondo poligono ci sono segmenti che attraversano il confine.
Proviamo
a prolungare i lati dei due poligoni: nel 1° poligono i prolungamenti non
attraversano la regione interna ed il poligono si dice convesso, nel 2°
poligono alcuni prolungamenti attraversano la regione interna ed il poligono si
dice concavo.