COMPETENZE
TRAGUARDI DI COMPETENZA
|
OBIETTIVI SPECIFICI
|
L’alunno riconosce e utilizza
rappresentazioni diverse di oggetti matematici (numeri decimali, frazioni,
percentuali, scale di riduzione).
|
|
PROBLEM SOLVING
Ho mangiato i 3/7 di una barra di cioccolata, ho mangiato
tutta la cioccolata? Quanta ne posso ancora mangiare? Perché?
SPIEGAZIONE: PRIMA FASE
Sul quaderno : i 3/8 di un campo sono coltivati ad insalata. Come possiamo rappresentare questa situazione?
Qual è la parte
coltivata? I 3/8
Qual è la parte non
coltivata? I 5/8
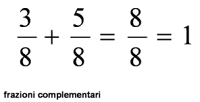
Se sommo le due parti
ottengo l’intero campo? Sì e allora posso dire che
Le frazioni che
insieme formano l’intero si dicono frazioni complementari.
SPIEGAZIONE: SECONDA FASE
Iniziamo il discorso sulle frazioni equivalenti, prendendo spunto dal fatto che molti alunni frequentano la piscina.
Queste sono le corsie di una piscina. Ecco quale distanza hanno già percorso alcuni alunni.
Angelica ha percorso i 2/4, Agnese 1/2, Anastasia 3/6 e Giorgia i 6/12.
Rappresentiamo sul quaderno
Cosa notiamo? Certo, osserviamo che le quattro bambine in realtà hanno percorso la stessa distanza. Quindi possiamo dire che 2/4, 1/2, 3/6 e 6/12 sono frazioni che hanno lo stesso valore, sono frazioni equivalenti.
Vediamo un altro esempio: se distribuiamo una uguale tavoletta di cioccolato a quattro bambini e poi osserviamo che Simone ne ha mangiato 1/3, Andrea i 2/6, Joan i 3/9 e Davide i 4/12, chi è stato più goloso e ne ha mangiato di più?
Anche in questo caso osserviamo che nessun bambino è stato più goloso degli altri, tutti e quattro hanno mangiato la stessa quantità della tavoletta di cioccolato.
Possiamo quindi dire che:
1/2 = 2/4 = 3/6 = 6/12
1/3 = 2/6 = 3/9 = 4/12
Le frazioni
equivalenti ad una data formano un insieme infinito, che si dice classe di
equivalenza. Come possiamo trovare le
classi di equivalenza?
Ricordando che la frazione corrisponde ad una divisione, possiamo capire che anche la frazione gode della proprietà invariantiva, per cui moltiplicando o dividendo sia il numeratore che il denominatore per uno stesso numero otteniamo altre frazioni equivalenti a quelle date.
Proviamo insieme a calcolare alcune frazioni equivalenti a quelle date.
ESERCIZI
Proponiamo attività individuali come le seguenti.
VERSO LE COMPETENZE
Marco ha incollato i 30/50 delle figurine dell'album. Esprimi in frazione quante sono le figurine che può ancora incollare.
Ecco le figurine incollate già da altri bambini su un album dello stesso tipo:
Giorgio 15/20, Elisa 15/25, Luca 2/5, Francesco 3/5, Tommaso 6/10.
Chi ha incollato un numero di figurine equivalente a quello di Marco?
Un test/gioco on line sulle frazioni
Vedi U. A. di riferimento