Matematica per gli insegnanti
L’addizione gode delle seguenti proprietà, che ci aiutano in molti casi a velocizzare e semplificare i calcoli:
· Commutativa: la somma di due o più addendi non cambia cambiando l’ordine degli addendi. Possiamo anche dire:
" a,b є N (leggiamo “Per qualunque numero a e b appartenente ad N”)
a + b = b + a
· Associativa: la somma di 3 o più addendi non cambia associando a 2 o più addendi la loro somma. Possiamo anche dire:
" a,b, c є N (leggiamo “Per qualunque numero a, b, c appartenente ad N”)
a + b + c = a + (b + c) = (a + b) + c
· Dissociativa: la somma di 2 o più addendi non cambia se scomponiamo un addendo in altri la cui somma sia uguale all’addendo stesso. Possiamo anche dire:
" a,b, c, d є N (leggiamo “Per qualunque numero a, b, c, d appartenente ad N”)
a + b = a + (c + d) con c + d = b
Matematica per gli alunni
COMPETENZE
|
ABILITA’
|
UNITA’
DI APPRENDIMENTO
|
Si muove con sicurezza
nel calcolo scritto e mentale con i numeri naturali e sa valutare
l’opportunità di ricorrere a una calcolatrice.
Sviluppa un atteggiamento positivo rispetto alla
matematica, attraverso esperienze significative.
|
- Al termine della classe terza l'alunno dovrà:
applicare le proprietà dell'addizione per facilitare il calcolo
orale e mentale.
|
PROPOSTA DIDATTICA
Cerchiamo di mettere in pratica il loro consiglio.
Chiariamo ai bambini cosa si intende parlando di proprietà.
Che cosa sono le proprietà di un’operazione? Sono delle caratteristiche che un’operazione possiede e che permettono di velocizzare il calcolo mentale.
Abbiamo già visto facendo osservazioni sulla tabella dell’addizione che l’addizione gode della proprietà commutativa.
Vediamo l’utilità della proprietà commutativa in 3 casi:
• 8 + 33 = 33 + 8 La proprietà commutativa ci permette di invertire l’ordine degli addendi e, per agevolare il calcolo, mettere prima il maggiore.
• 32 + 16 + 28 = 32 + 28 + 16 Possiamo spostare gli addendi e mettere vicini quelli amici
• Per eseguire la prova dell’addizione
Partiamo da un'altra situazione problematica.
Dobbiamo fotocopiare un avviso per le tre classi terze del plesso: sapendo che in 3A ci sono 24 alunni, in 3B 27 ed in 3C 16, quante fotocopie dovremo fare?
Rappresentiamo con i diagrammi la situazione, vedendo i tre modi possibili di associare gli addendi.
Abbiamo applicato in questi casi la proprietà associativa che ci permette di sostituire due o più addendi con la loro somma senza che cambi il risultato.
Chiediamo a questo punto qual è, secondo il parere degli alunni, il modo più semplice di calcolare fra i tre casi, in modo da evidenziare l'utilità di associare quegli addendi che facilitano il calcolo perchè hanno alle unità i numeri amici del dieci.
Trascriviamo il caso in cui abbiamo associato 24 e 16, usando questa volta le parentesi invece del diagramma.
Vediamo altri esempi insieme e poi facciamo eseguire un esercizio individuale.
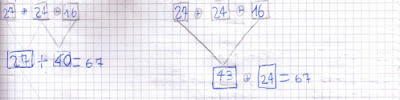
Ieri una vostra compagna non riusciva a trovare il risultato di 24 + 18. Come potremmo aiutarla? Sentiamo i suggerimenti che arrivano dagli alunni e concentriamo l'attenzione su due in particolare (se non emergono dagli alunni, saremo noi a sollecitare l'attenzione su di essi).
Nella mia classe Giorgia ha proposto di scomporre il secondo addendo e di aggiungere prima 10 e poi 8. Anastasia invece propone di sommare le decine dei due addendi e poi di aggiungere la somma delle unità. Rappresentiamo i due diversi modi di procedere.
In entrambi i casi abbiamo applicato la proprietà dissociativa dell’addizione: in un’addizione posso sostituire un addendo con altri la cui somma sia uguale all’addendo stesso.
Vediamo altre addizioni insieme usando sempre entrambi i modi sopra descritti:
25 + 42 = (25 + 40) + 2 oppure 20 + 5 + 40 + 2 = (20 + 40) + (5 + 2) = 60 + 7 = 67
127 + 54 = 127 + 50 + 4 oppure 100 + 20 + 7 + 50 + 4 = (100+20+50) + (7+4)=170+11=181
358 + 226=358+200+20+6 oppure 300+50+8+200+20+6=(300+200)+(50+20)+(8+6)
Per gli esercizi individuali ho lasciato libertà di scelta, in modo che ogni alunno usasse la strategia più adeguata al proprio modo di contare. Nell'esempio che qui propongo, l'alunna ha optato per la strategia di dissociare il secondo addendo, altri invece hanno scelto di dissociare entrambi gli addendi, alcuni alunni hanno usato un po' l'uno un po' l'altro sistema.
PROPOSTA PER ATTIVITA' DI LABORATORIO
A gruppi i bambini possono affrontare il seguente quiz.
Una verifica scritta dell'U. A. da stampare
Un test sui contenuti dell'unità n° 2: addizione e proprietà