Matematica per gli insegnanti
Esaminiamo il caso in cui i due insiemi sono disgiunti.
Consideriamo l’insieme A = {a/a è una vocale} e l’insieme B = {b/b è una delle prime quattro consonanti dell’alfabeto italiano}.
Per elencazione:
A = {a; e; i; o ; u}
B = {b; c; d; f }
Vediamo graficamente l’intersezione dei due insiemi.
AÇB = Æ - L’intersezione è un insieme vuoto perché non ci sono elementi in comune.
Vediamo ora il caso di due insiemi intersecati.
Consideriamo per elencazione:
A = {Francia; Germania; Italia; Gran Bretagna; Svezia; Polonia}
B = {Spagna; Francia; Italia; Tunisia; Grecia; Egitto}
Vediamo graficamente l’intersezione dei due insiemi.
AÇB = { Francia; Italia} - L’intersezione è l’insieme con gli elementi comuni Francia ed Italia.
Riflettiamo infine sul caso in cui un insieme è incluso nell'altro perché è un suo sottoinsieme proprio.
Consideriamo per elencazione:
A = {Pirlo; Chiellini; Pazzini; Cassano; Buffon; De Rossi}
B = {Pirlo; Chiellini; Buffon}
AÇB = {Pirlo; Chiellini; Buffon}- L’intersezione è l’insieme B perché sono gli elementi di B in comune con gli elementi di A.
Matematica per gli alunni
COMPETENZE
|
ABILITA’
|
UNITA’
DI APPRENDIMENTO
|
Ricerca dati per ricavare informazioni e costruisce
rappresentazioni (tabelle e grafici). Ricava informazioni da dati
rappresentati in tabelle e grafici.
Costruisce ragionamenti formulando ipotesi, sostenendo le
proprie idee e confrontandosi con il punto di vista di altri.
|
- Al termine della classe terza l'alunno dovrà:
classificare elementi in
base a due attributi utilizzando
rappresentazioni opportune; indicare gli attributi di una
classificazione; rappresentare insiemi con l’uso di diagrammi (Venn, Carrol,
ad albero); saper utilizzare il connettivo “e”.
|
PERCORSO DIDATTICO
Br1 e Bass8 ci hanno mandato delle belle illustrazioni, affinché possiamo giocarci e mi hanno suggerito un gioco interessante. Ecco cosa mi hanno detto di fare: “ Le immagini dovrai stampare e nei diagrammi di Venn le dovrai sistemare”.
Distribuiamo ad alcuni alunni una serie di illustrazioni, dando l’incarico di sistemarle una per una al posto giusto nei diagrammi di Venn, come indicato in seguito. Fai clic per stampare le illustrazioni.
Usciamo nell'atrio dove lo spazio è maggiore.
Formiamo sul pavimento due diagrammi di Venn: su uno mettiamo il cartellino “Insieme di frutti” e sull'altro mettiamo il cartellino “Insieme di cose rosse” e cominciamo ad inserire le immagini. Per alcune non ci saranno difficoltà.
Per altre immagini dobbiamo fare attenzione: “la mela è un frutto e quindi dovrei metterla nell'insieme dei frutti, ma è anche rossa quindi dovrei metterla anche nell'insieme delle cose rosse”. Come fare? Lasciamo che gli alunni riflettano e se non lo propongono loro, memori di lavori già fatti lo scorso anno, proponiamo noi di avvicinare i due diagrammi e di intersecarli. Come chiameremo questa nuova regione? Prepariamo ed inseriamo il relativo cartellino. In questo modo potremo sistemare tutti i frutti non rossi, i frutti rossi, le cose di colore rosso. E dove metteremo l’ombrello blu?
Rientriamo in classe e proseguiamo il lavoro sul quaderno. Rappresentiamo con i diagrammi di Venn.
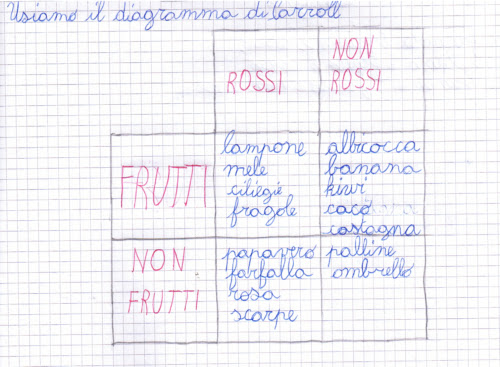
Rappresentiamo con il diagramma di Carroll.
Rappresentiamo con il diagramma ad albero.
Scriviamo alcune frasi usando il connettivo e: la fragola è frutto e rosso, la mela è frutto e rosso, la banana è frutto e non è rosso.
Vediamo ora la tavola della verità per la congiunzione “e”.
Br1 ha promesso a Bass8: “Per Natale ti porto a sciare e a pattinare”.
Se non lo porta né a sciare né a pattinare ha mantenuto la promessa?
Se lo porta a sciare ma non a pattinare ha mantenuto la promessa?
Se lo porta a pattinare ma non a sciare ha mantenuto la promessa?
Se lo porta sia a sciare che a pattinare ha mantenuto la promessa?
Rappresentiamo la tavola della verità usando una pallina verde per indicare il vero ed una pallina rossa per indicare il falso.
Riflettiamo sul fatto che un enunciato con due condizioni legate dalla congiunzione e è vero solo se sono vere entrambe le condizioni.
Propongo poi una scheda di lavoro. Se vuoi stamparla fai clic qui.
PROPOSTA PER ATTIVITA' DI LABORATORIO