"Che cos'è una superficie? E' maggiore la superficie del banco o quella della cattedra? Qual è la superficie minore tra quella del quadernone e quella del diario? E' maggiore la superficie del quaderno di Elisa o quella del quaderno di Alice?"
Quest'ultimo caso ci darà la possibilità di affermare che le figure con la stessa estensione si dicono equiestese o equivalenti.
Disegniamo alla lavagna e sul quaderno due figure congruenti: sono anche equivalenti? Vedendo anche altri esempi giungiamo ad affermare che, se due figure sono congruenti, sono anche equivalenti.
Disegniamo poi due figure equivalenti ma non
congruenti. Sono congruenti? Sono equivalenti? Le figure equivalenti possono
anche non essere congruenti.
Disegniamo infine due figure come quelle che vedi (figure E ed F). Sono congruenti? Sono equivalenti? Le due figure non sono congruenti e non sono equivalenti.
L'unità di misura delle superfici è un quadrato con i lati lunghi un metro, si chiama metro quadrato e si indica con m2. Realizziamo il metro quadrato usando un cartellone murale e disponiamolo sul pavimento. Chiediamo agli alunni di indicare superfici maggiori o minori del metro quadrato.
Propongo un lavoro riassuntivo sui sottomultipli del m2
A questo punto gli alunni non avranno difficoltà a capire quali saranno i multipli del m2.
Proviamo quindi a costruire la tabella delle misure di superficie, chiedendo per ogni misura a quanti metri quadrati corrisponde, cioè quante volte la misura è più grande o più piccola rispetto al metro quadrato.
Come si fa a misurare una superficie? Ricordiamo
che misurare una superficie significa vedere quante volte una superficie
campione è contenuta nella superficie da misurare. Di quale forma sarà la
superficie campione?
Qual è la forma della superficie più adatta per ricoprire altre superfici?
Ascoltiamo le risposte dei nostri alunni, senz'altro ci sarà chi individua il quadrato come forma più idonea.
Distribuiamo allora ad ogni coppia di bambini 2 quadrati di diverse dimensioni (un bambino avrà un
quadrato con il lato di 10 cm e l’altro un quadrato con il lato di 7 cm ed
usiamolo per misurare la superficie del banco). Noteremo risultati diversi e
quindi la necessità di un’unità di misura convenzionale uguale per tutti.
Evidenziamo poi la necessità di un'unità di misura più piccola del metro quadrato. Quale potrà essere? Quale sarà la forma? Certo, sarà un quadrato e la grandezza sarà di un dm per ogni lato. Allo stesso modo presentiamo il centimetro quadrato ed il millimetro quadrato.
Utilizziamo ora un foglio di carta millimetrata. Per stamparlo puoi fare clic su questo link: https://secondabgp.files.wordpress.com/2010/12/carta-millimetrata-a4.pdf
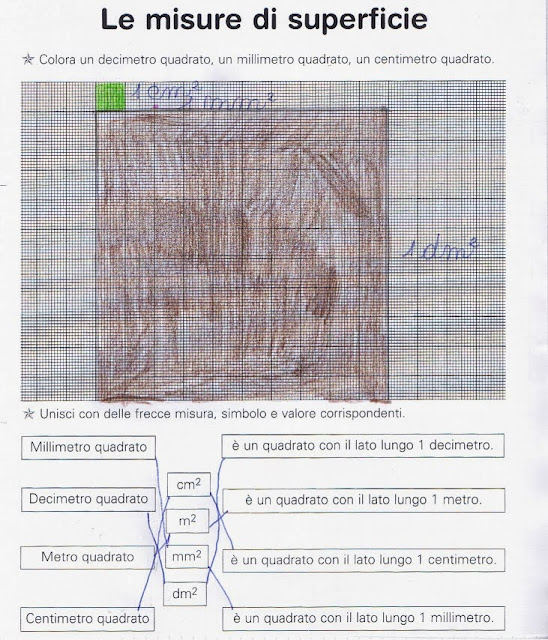
Disegniamo
e coloriamo il dm2, il cm2 ed il mm2 sulla scheda.
Utilizzando i decimetri quadrati che puoi stampare qui proviamo a ricoprire la base e l'altezza del metro quadrato. Capiremo così che in un metro quadrato ci sono 100 decimetri quadrati, quindi 1 m2 = 100 dm2.
Facciamo la stessa cosa con i centimetri quadrati che puoi stampare qui, ricoprendo base ed altezza del decimetro quadrato. Notiamo
che in un decimetro quadrato ci sono 100 centimetri quadrati, quindi 1 dm2 = 100 cm2, 1 m2 = 10 000 cm2.
Notiamo infine che in un centimetro quadrato ci sono 100 millimetri quadrati, quindi 1 cm2 = 100 mm2, 1 dm2 = 10 000 mm2, 1 m2 = 1000000 mm2. Osserviamo anche la
differenza con le misure lineari.
Propongo un lavoro riassuntivo sui sottomultipli del m2
A questo punto gli alunni non avranno difficoltà a capire quali saranno i multipli del m2.
Proviamo quindi a costruire la tabella delle misure di superficie, chiedendo per ogni misura a quanti metri quadrati corrisponde, cioè quante volte la misura è più grande o più piccola rispetto al metro quadrato.
Noteremo che ogni misura di
superficie è 100 volte più piccola della precedente a sinistra e 100 volte più
grande della seguente a destra.
Siccome segue la base 100, ogni
misura di superficie si esprime con due cifre, quella delle decine e quella
delle unità.
Dopo aver fatto compiere alla lavagna esercitazioni, propongo l'esecuzione di tre schede: fai clic per stampare la prima.
Fai clic per stampare la seconda.
Ed ecco una terza scheda con esercizi tratti dalle prove Invalsi degli anni precedenti: fai clic per stamparla.
