Matematica per gli insegnanti
La capacità di eseguire le quattro operazioni in
colonna deve essere coltivata e potenziata in modo molto graduale. Naturalmente
l’importanza della costruzione degli algoritmi di calcolo delle quattro
operazioni non riveste più la valenza ed il significato che poteva avere in
precedenti periodi storici: non è più l’utilità pratica ad essere il fine del
nostro insegnamento, sappiamo benissimo che calcolatrici e computer possono
svolgere questo ruolo in modo molto più veloce ed efficace di quanto possa fare
la mente umana. Perché allora continuare ad insegnare le operazioni in colonna
a scuola? Secondo me sono possibili diverse risposte, anche semplificando
necessariamente un po’ la complessità del discorso.
Poiché è la mente umana che
pensa e progetta la costruzione delle macchine, ritengo siano le macchine a
dover dipendere dall’uomo e non il contrario: saper calcolare indipendentemente
dalle macchine, in questa prospettiva, è una forma di libertà dal
condizionamento degli strumenti.
In secondo luogo si tratta di sviluppare la
capacità transdisciplinare di eseguire in modo chiaro, ordinato e corretto una
sequenza di azioni.
Contrariamente a quanto avveniva in passato,
ritengo però necessario che l’acquisizione degli automatismi di calcolo avvenga
non solo meccanicamente, ma in modo che gli alunni capiscano il significato di
ciò che stanno facendo. Operiamo quindi con gradualità utilizzando una
pluralità di strumenti: materiale non strutturato, regoli, abaco, ecc.
Importante sarà anche guidare gli alunni, in una fase successiva, ad esprimere
risultati stimati o a valutare tra stime di possibili risultati.
E’ inutile ribadire ancora una volta l’importanza, invece,
del calcolo mentale, a cui si dovrebbe dedicare un po’ di attenzione quasi
tutti i giorni
Matematica per gli alunni
COMPETENZE
|
ABILITA’
|
UNITA’
DI APPRENDIMENTO
|
Si muove con sicurezza
nel calcolo scritto e mentale con i numeri naturali e sa valutare
l’opportunità di ricorrere a una calcolatrice.
Sviluppa un
atteggiamento positivo rispetto alla matematica, attraverso esperienze
significative, che gli hanno fatto intuire come gli strumenti matematici che
ha imparato ad utilizzare siano utili per operare nella realtà.
|
- Al termine della classe terza l'alunno dovrà:
eseguire addizioni in
colonna entro il mille con e senza cambi usando i corretti algoritmi .
|
PROPOSTA DIDATTICA
Una premessa per chiarire il lavoro. Ho ideato il sistema delle carte stradali per dare un motivo agli alunni per effettuare e ripassare le addizioni in colonna: si tratta di calcolare vari itinerari per vedere quanti km si dovranno fare. Propongo all’attenzione degli alunni sei casi corrispondenti ad altrettante cartine: nel primo non c’è cambio, nel secondo un cambio dalle unità alle decine, nel terzo un cambio sempre dalle u alle da ma con tre addendi, nel quarto un cambio dalle da alle h, nel quinto ci sono 2 cambi, così come nel sesto, ma con tre addendi. Se vuoi stampare le sei carte fai clic qui.
Finalmente Br1 ed il Bass8 arrivano sulla Terra e, guarda caso, giungono proprio in Italia. La loro astronave atterra nell’aeroporto di Roma e subito è circondata da una moltitudine di persone che gridano:”Sono arrivati i marziani! I marziani a Roma!”. Ma noi sappiamo che i due non sono marziani ma provetti matematici provenienti dalla Galassia Matematica: infatti immaginatevi la delusione della gente quando vede che i “marziani” non hanno il corpo verde e sono fatti di carne, ossa e cervello.
Br1 ed il Bass8 rimangono colpiti dall’accoglienza ricevuta e si chiedono: "Sono questi i terrestri che siamo venuti a studiare? Poveri noi!"
“Però non devono essere cattivi, mi paiono solo tanto curiosi.”
“Chi lo sa! Dovremo metterci d’impegno per capirli”
“Secondo me il modo migliore per capirli è cercare di fare come loro”
“E allora chiediamo cosa stanno facendo qui”.
E così fanno ed in questo modo vengono a sapere che la gente è qui in aeroporto soprattutto per viaggiare, per partire e per ritornare dalle vacanze.
“Allora andiamo anche noi in vacanza. Come si fa?”
“Prima bisogna scegliere una destinazione e poi partire”
“Siamo fortunati, mentre eravamo in volo ho programmato il navigatore interstellare Tam Tam che mi ha sfornato parecchie carte con degli itinerari che possiamo fare!”
“Io però vorrei sapere quanti km dovrò fare, perché non sono molto in gamba guidare quelle scatole d’acciaio che qui chiamano macchine. Dammi la prima carta”
“Eccola” (si tratta di addizione senza cambio)
“Il primo viaggio ci porterà da Roma a L’Aquila e poi a Pescara”
“Calcoliamo i km. Ah, Bass8, ricordiamoci che qui siamo nel paese del dieci e che quindi bisogna cambiare ogni volta che si hanno 10 elementi”
E Bass8: “Io ho un metodo infallibile e voglio farlo conoscere anche ai nostri amici, i bambini di terza che stanno seguendo le nostre avventure. Meritano un aiuto!”
“Allora, vediamo un po’, da Roma a L’Aquila ci sono 116 km, da L’Aquila a Pescara 113 km. Quanti saranno in tutto?”
“Ecco come fare e non sbagliare con il sistema di Bass8. Comincia dalle colonna delle unità, cerchiala in azzurro, conta le unità, sono meno di 10 e quindi non c’è nessun cambio. Passa alla colonna delle decine, cerchiala in rosso, conta le decine, sono meno di 10 e non c’è cambio. Infine passa alla colonna delle centinaia, cerchiala in verde, conta le centinaia e scrivi quanto sono. Semplice, no? Ah, dimenticavo, c’è un modo per controllare se la tua operazione è corretta: devi fare la prova, applicando la proprietà commutativa e cambiando l’ordine degli addendi e poi controlla se le due somme sono uguali.”
Rappresentiamo sul quaderno ed eseguiamo due operazioni simili (naturalmente senza ripetere tutta la procedura): 21 + 955, 212 + 141
Vediamo la seconda carta (un cambio dalle u alle da)
Ripetiamo la procedura: da Roma a Napoli 226 km, da Napoli a Bari 264 km. Quanti km in tutto?
“Ecco come fare e non sbagliare con il sistema di Bass8. Comincia dalle colonna delle unità, cerchiala in azzurro, conta le unità, sono 10 e quindi dobbiamo cambiare in una decina e ci restano 0 unità. Passa alla colonna delle decine, cerchiala in rosso, conta le decine, sono meno di 10 e non c’è cambio. Infine passa alla colonna delle centinaia, cerchiala in verde, conta le centinaia e scrivi quanto sono”.
Rappresentiamo sul quaderno ed eseguiamo due operazioni simili: 63 + 28, 328 + 246
Consegniamo la terza carta (un cambio dalle u alle da con tre addendi)
Allora: da Roma a Napoli 226 km, da Napoli a Catanzaro 409 km, da Catanzaro a Catania 253 km. Quanti km in tutto?
“Ecco come fare e non sbagliare con il sistema di Bass8. Comincia dalle colonna delle unità, cerchiala in azzurro, conta le unità, sono 18 e quindi dobbiamo cambiare in una decina e ci restano 8 unità. Passa alla colonna delle decine, cerchiala in rosso, conta le decine, sono meno di 10 e non c’è cambio. Infine passa alla colonna delle centinaia, cerchiala in verde, conta le centinaia e scrivi quanto sono”.
Rappresentiamo sul quaderno ed eseguiamo due operazioni simili: 127 + 35 + 124, 328 + 419 + 252
Vediamo la quarta carta (un cambio dalle da alle h)
Ripetiamo la procedura: da Roma a Firenze 283 km, da Firenze a Genova 231 km. Quanti km in tutto?
“Ecco come fare e non sbagliare con il sistema di Bass8. Comincia dalle colonna delle unità, cerchiala in azzurro, conta le unità, sono meno di 10 e quindi non dobbiamo cambiare. Passa alla colonna delle decine, cerchiala in rosso, conta le decine, sono 11 e quindi dobbiamo cambiare in 1 centinaio e ci resta 1 decina. Infine passa alla colonna delle centinaia, cerchiala in verde, conta le centinaia e scrivi quanto sono”.
Rappresentiamo sul quaderno ed eseguiamo due operazioni simili: 657 + 82, 392 + 137
Vediamo la quinta carta (due cambi).
Ripetiamo la procedura: da Roma a Perugia 182 km, da Perugia a Bologna 258 km. Quanti km in tutto?
“Ecco come fare e non sbagliare con il sistema di Bass8. Comincia dalle colonna delle unità, cerchiala in azzurro, conta le unità, sono 10 e quindi dobbiamo cambiare in una decina e ci restano 0 unità. Passa alla colonna delle decine, cerchiala in rosso, conta le decine, sono 13 e quindi dobbiamo cambiare in 1 centinaio e ci restano 3 decine. Infine passa alla colonna delle centinaia, cerchiala in verde, conta le centinaia e scrivi quanto sono”.
Rappresentiamo sul quaderno ed eseguiamo due operazioni simili: 75 + 89, 258 + 687
Infine vediamo la sesta carta (due cambi con tre addendi).
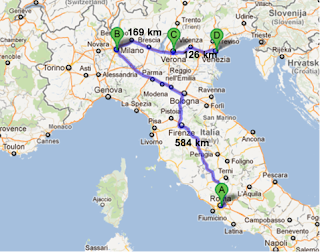
Ripetiamo la procedura: da Roma a Milano 584 km, da Milano a Verona 169 km, da Verona a Venezia 126 km. Quanti km in tutto?
“Ecco come fare e non sbagliare con il sistema di Bass8. Comincia dalle colonna delle unità, cerchiala in azzurro, conta le unità, sono 19 e quindi dobbiamo cambiare in una decina e ci restano 9 unità. Passa alla colonna delle decine, cerchiala in rosso, conta le decine, sono 17 e quindi dobbiamo cambiare in un centinaio e ci restano 7 decine. Infine passa alla colonna delle centinaia, cerchiala in verde, conta le centinaia e scrivi quanto sono”.
Rappresentiamo sul quaderno ed eseguiamo due operazioni simili: 32 + 334 + 289, 6 + 197 + 85.
Alcune interessanti attività on line sono quelle che si possono trovare sul sito Baby Flash
oppure sul sito di Interdidactica.
oppure sul sito di Interdidactica.
PROPOSTE PER ATTIVITA' DI LABORATORIO
425 + 186 = ………….. (L)
336 + 259 = ………….. (A)
179 + 458 =………….. (N)
345 + 274 = ………….. (O)
458 + 232 = ………….. (I)
448 + 73 = ………….. (N)
67 + 198 = ………….. (P)
349 + 87 + 123 = ………….. (T)
2 + 57 + 138 = ………….. (I)
302 + 146 + 31 = ………….. (A)