I numeri oltre il mille - classe terza

Matematica per gli insegnanti

Il nostro sistema di numerazione è posizionale perché il valore delle cifre dipende dalla posizione che occupano nel numero.

Il nostro sistema di numerazione è decimale perché si raggruppa per dieci, in questo modo:

·        Le cifre da 0 a 9 sono chiamate unità del 1° ordine

·        10 unità del 1° ordine formano una decina (unità del 2° ordine)

·        10 unità del 2° ordine formano un centinaio (unità del 3° ordine)

·        10 unità del 3° ordine formano un migliaio (unità del 4° ordine)

·        10 unità del 4° ordine formano una decina di migliaia (unità del 5° ordine)

·        10 unità del 5° ordine formano un centinaio di migliaia (unità del 6° ordine)

e così via.

Abbiamo quindi vari ordini, che vengono raggruppati per 3 in gruppi, chiamati classi, per renderne più facile la lettura e la scrittura.

Consideriamo, ad esempio, il numero

13 045 523

e vediamo due modi in cui è possibile indicare il valore di ogni cifra. Possiamo scomporre così:

oppure  mediante la scomposizione polinomiale:

3 + 2 x 10 + 5 x 100 + 5 x 1 000 + 4 x 10 000 + 3 x 1 000 000 + 1 x 10 000 000

Finora abbiamo parlato di numeri interi positivi e sappiamo che sono infiniti: questi numeri si chiamano naturali ed appartengono all’insieme N dei numeri naturali che è quindi un insieme ordinato (posso stabilire con certezza quale numero precede o segue un altro) ed infinito che si può rappresentare nei soliti 3 modi:

       per elencazione            N = {0; 1; 2, 3, …….}

       per caratteristica          N = {x/x è un numero naturale}

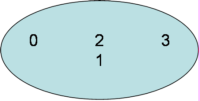
       graficamente con il diagramma di Eulero - Venn

Matematica per gli alunni

COMPETENZE	ABILITA’	UNITA’ DI APPRENDIMENTO
Sviluppa un atteggiamento positivo rispetto alla matematica. Riconosce ed utilizza rappresentazioni diverse di oggetti matematici.	-  Al termine della classe terza l'alunno dovrà: leggere e scrivere i numeri naturali in notazione decimale, avendo consapevolezza della notazione posizionale; confrontare e ordinare i numeri naturali fino a mille; conoscere il valore posizionale delle cifre; scomporre i numeri fino a mille nelle corrispondenti somme di migliaia, centinaia, decine unità e ricomporli; individuare il significato e utilizzare correttamente lo zero e il valore posizionale delle cifre; individuare successioni numeriche data una regola e viceversa; numerare in ordine progressivo e regressivo.	Unità n° 4: La montagna

PERCORSO DIDATTICO

Lo scopo di questa prima fase del lavoro è quello comprendere la struttura ed il valore posizionale dei numeri oltre il mille: a tal fine ci soffermeremo soprattutto su alcuni passaggi critici (1 001, 1 010, 1 011, 1 099, 1 100, 1 101, 1 199, 1 200, 1 999, 2 000), evidenziandoli attentamente con l'uso dell'abaco, dei Bam e della rappresentazione grafica.
Finalmente Bruno ha convinto Bassotto a salire sulla funivia. La funivia parte da un’altitudine di 1000 metri.

Vediamo di rappresentare mille usando l’abaco ed il materiale multibase.
Aggiungiamo un’unità.
Dopo 1 m a quale altezza saranno?
Rappresentiamo sempre usando l’abaco ed i BAM e registriamo sul quaderno.
Scriviamo i numeri seguenti fino a 1009
Dopo 10 metri quale altezza avranno raggiunto? E dopo 11 metri?
Rappresentiamo sempre usando l’abaco e BAM e registriamo sul quaderno
Scriviamo i numeri seguenti fino a 1020
Oralmente e scrivendo i numeri alla lavagna: 1000 + 30, 1000 + 40, 1000 + 50, ecc…
Dopo 99 metri saranno arrivati a ………
Salendo ancora di un metro giungeranno ad un’altitudine di …………

Prosegue la salita ancora di un metro. Ora sono giunti a quota 1101 che rappresentiamo su abaco, multibase e quaderno.

Scriviamo i numeri seguenti fino a 1120
Dopo 199 metri saranno arrivati a ………
Salendo ancora di un metro giungeranno ad un’altitudine di …………

Oralmente e scrivendo i numeri alla lavagna: 1000 + 200, 1000 + 300, 1000 + 400, 1000 + 500, ecc

Dopo 999 metri saranno arrivati a ………
Salendo ancora di un metro giungeranno ad un’altitudine di …………


Rappresentiamo sempre usando l’abaco ed il multibase e registriamo sul quaderno.
Oralmente e scrivendo i numeri alla lavagna: 1000 + 1000, 1000 + 2000, 1000 + 3000, 1000 + 4000, 1000 + 5000, ecc

A questo punto prepariamo dei cartellini con i numeri da 0 a 9, posiamoli capovolti sulla cattedra, chiamiamo i bambini a gruppi di 4, ogni bambino prende un cartellino e si dispone in fila guardando il suo numero e mostrandolo ai compagni, i quali dovranno leggere il numero formato dai 4 bambini. Successivamente i 4 alunni cambieranno alcune volte l’ordine della loro posizione ed i compagni dovranno ogni volta leggere il numero che si sarà formato.

Propongo due schede in cui gli alunni dovranno disegnare sull'abaco le quantità indicate e, viceversa, dovranno scrivere in cifre le quantità rappresentate sull'abaco. Fai clic sui link per stampare le schede: scheda 1 e scheda 2.
Proponiamo anche un esercizio sul quaderno: utilizzando ogni volta tutte le cifre 1 – 5 – 6 – 0 scrivi almeno sei numeri diversi in cifre ed in lettere.

Propongo un video di Camillo Bortolato per la lettura delle quantità oltre il mille mediante analogie iconiche con le case e le finestre e per esercizi di calcolo mentale senza numeri scritti nell'ordine del migliaio.




Una verifica scritta da stampare

Un test sui contenuti dell'unità n° 4: il migliaio

Ulteriori risorse dal Web