Probabilmente qualche lettore del blog si è accorto che gli argomenti didattici che sto sviluppando non sono in sintonia cronologica con la scansione temporale pubblicata nel sito. Infatti la mia attività è in leggero ritardo rispetto a ciò che prevedevo. Questo mi induce ad alcune considerazioni, che potrebbero essere utili anche per i lettori del blog. Prevedere una scansione temporale degli argomenti da affrontare nel corso dell’anno scolastico può essere un valido modo di procedere, a condizione di gestire la cosa con sufficiente elasticità e di essere previdenti nella programmazione tenendo conto di alcune variabili. Io, ad esempio, ho messo molta carne al fuoco nel primo quadrimestre sia perché lo ritengo il periodo più proficuo didatticamente sia perché la nostra scuola nel 2° quadrimestre è molto assorbita dalle preparazioni delle recite teatrali di fine anno che in qualche modo incidono sull’iter didattico.
Le variabili che intervengono nel processo di apprendimento sono però molte e non è possibile prevederle tutte a priori. Non avevo previsto le difficoltà incontrate nel lavoro sulle sequenze e numerazioni, che mi ha quindi richiesto molto più tempo di quanto preventivato. In ogni caso i tempi ed i ritmi da seguire ci sono dettati dai risultati e dai modi di apprendimento da parte dei nostri alunni: il vero termometro è questo. Non drammatizzo quindi il ritardo, lo recupereremo in seguito oppure faremo ciò che sarà possibile fare. Invito dunque i lettori del blog, che ultimamente si sono dimostrati molto interessati alla sequenza temporale delle attività, a considerare questa scansione come un promemoria che poi dovrà essere necessariamente modificato e contestualizzato.
Dalle numerose attività svolte negli ultimi giorni a proposito di sequenze numeriche, nella mia classe è emersa qualche difficoltà soprattutto nelle numerazioni decrescenti. Prendo quindi spunto da ciò per rivedere con gli alunni i meccanismi di calcolo relativi alla sottrazione. Inizialmente opereremo entro il 20 con l’obiettivo di oliare quei meccanismi che poi utilizzeremo prossimamente per i numeri entro il 100.
Oggi, venerdì, è uno dei giorni in cui abbiamo educazione motoria ed i giochi che si fanno in questa occasione sono sempre un ottimo inizio per la matematizzazione della realtà.
Ad esempio, in un gioco in palestra la squadra chiamata dei Leoni ha fatto 6 canestri, quella delle Tigri ne ha fatti 9. Quanti punti in più ha fatto la squadra delle Tigri?
L’operazione risolutiva, individuata dai bambini, è 9 – 6. Quasi tutti hanno detto il risultato senza esitazioni, il problema è il “quasi”. Vediamo quindi di aiutare chi è ancora un po’ in difficoltà.
Rivediamo il fatto che possiamo calcolare ricordando i risultati a memoria, usando le dita in modo corretto, con i regoli e con la linea dei numeri. Dopo alcuni esempi insieme alla lavagna facciamo calcolare gli alunni, utilizzando varie situazioni di calcolo possibili: entro la prima decina, i numeri amici del 10 nella sottrazione (es. 10 – 8), sottrazioni con risultato uguale alla decina (es. 16 – 6), sottrazioni nell’ambito della seconda decina (es. 17 – 5), con il passaggio della decina.
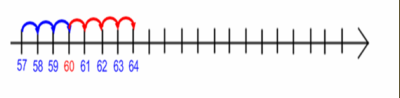
Il primo lavoro, che vedete sopra, ci ha permesso di ripassare le sottrazioni nella prima decina. Le attività sono proseguite vedendo come utilizzare i numeri amici del 10 anche per eseguire sottrazioni e ripassando le sottrazioni con risultato uguale alla decina.
Anche per le sottrazioni nell’ambito della seconda decina è utile ricordare che è possibile usare le dita se non si ricorda il risultato a memoria, ma è possibile anche seguire un’altra strada. Se, ad esempio, devo scoprire il risultato di 17 – 4 possiamo far riflettere gli alunni, eventualmente anche con l’aiuto dei regoli o dell’abaco, che 17 = 1 da e 7 u e se togliamo 4 u da 7 u restano 1 da e 3 u. Proponiamo alcuni calcoli da effettuare sul quaderno, ad esempio:
19 – 5
17 – 2
18 – 7
16 - 4
19 – 7
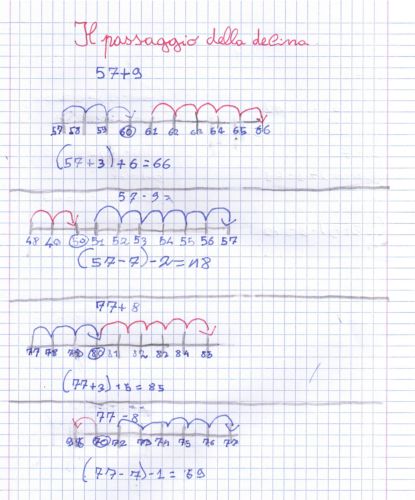
Affrontiamo ora le sottrazioni con il passaggio della decina. L’argomento è stato già illustrato in prima, ma dovremo senz’altro ripassarlo. Procediamo con i regoli o con l’abaco e con la linea dei numeri.
Se dobbiamo eseguire 15 – 9 formiamo il numero 15 ed iniziamo a togliere le 5 unità. 
Ci resta una decina che dobbiamo cambiare in 10 unità per poter togliere altre unità. Effettuato il cambio potremo togliere le restanti 4 unità.
Svolgiamo qualche esempio insieme: chi pensa di aver compreso può operare solo simbolicamente con i numeri, chi non è ancora sicuro potrà aiutarsi con i regoli o con la linea dei numeri.
