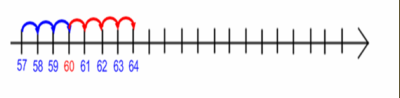
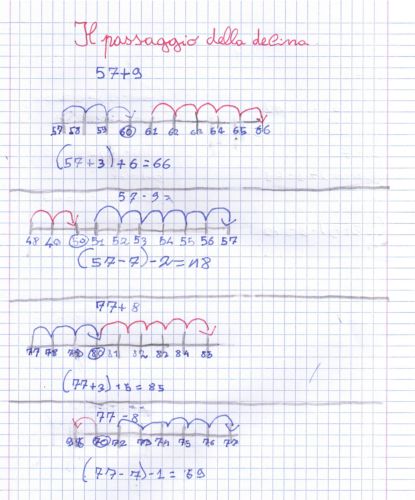
Propongo qui un necessario esercizio riassuntivo sui casi finora affrontati di calcolo mentale (addizione e sottrazione) od in riga con numeri entro il centinaio.
Prima di ogni altra cosa ecco una tabella con i principali casi affrontati.

Parto come faccio spesso da un breve racconto.
Il pirata Testavuota non riesce più a trovare il tesoro nascosto perché deve decifrare una mappa, ma per riuscirci deve prima risolvere alcune operazioni ed essendo "Testavuota" non ce la fa. Lo aiuteremo noi eseguendo i calcoli.
Consegniamo agli alunni un reticolo, come questo. Per stamparlo fai clic qui o sull'immagine.
A questo punto presentiamo agli alunni alcune batterie di operazioni. Ogni operazione sarà accompagnata da una lettera dell'alfabeto. Una volta che gli alunni avranno scritto tutti i risultati inseriranno in una tabella le lettere corrispondenti ai risultati ed otterranno così le indicazioni per procedere sul reticolo e trovare il tesoro.
Ecco la prima batteria di operazioni, al termine della quale otterranno l'indicazione "tre passi avanti" che eseguiranno sul reticolo.
Al termine della seconda batteria, l'indicazione ottenuta sarà : "sette passi in basso".
Dopo la terza batteria gli alunni vedranno l'indicazione: "sei passi in avanti".
E, infine, dopo la quarta ed ultima batteria otterranno l'indicazione: "due passi in alto".
Eseguendo sul reticolo tutti gli spostamenti indicati gli alunni arriveranno al tesoro.
Puoi stampare la scheda con tutte le operazioni e le tabelle facendo clic qui.
Ecco come gli alunni hanno eseguito il lavoro proposto.